吴江-社会网络计算基础理论与实践

2022-03-21

备注:: 社会网络计算方法、[[R语言社会网络分析]]
附件:: [[社会网络计算基础理论与实践.pdf]]

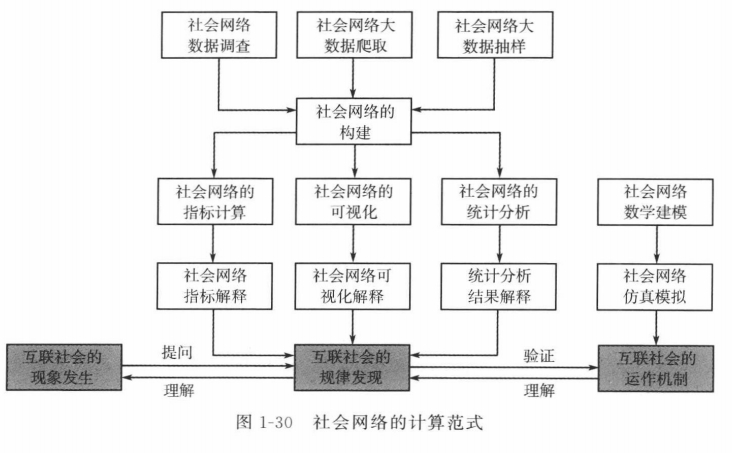
社会网络的计算范式
三元闭包
- 三元闭包原理
- 网络边和节点的演化
  - 增加节点和边
  - 节点的访问
- 聚集系数：
  - 点聚集系数：计算三元闭包的强度，节点A的任意两个朋友彼此也是朋友的概率，节点朋友圈的紧密程度，实际相邻点对/理论相邻点对，即：边/点对(Newman, 2003)
  - 全局聚集系数：\(C=\frac{\text{三角形数}×3}{\text{连通三元组数}}\)，有共同朋友的两个人中，彼此也是朋友的比例，也就是共被引的文献之间存在引用关系的比例。
  - R语言igraph包计算聚集系数
嵌入性
- Granovetter(1985)经济学与社会学的爱恨情仇，新社会经济学格兰诺维特的嵌入 - 哔哩哔哩专栏
结构洞
- 移除某个点，会使得网络的连通分量增加。
  - 聚集系数不高
  - 信息获取优势
  - 创造性放大优势
    - 同质信息——异质信息
  - 社交把关的权力
  - 介数，参见[[R语言社会网络分析#^6126d7]]
- 使用R语言计算中心度
  - 参考书：[[社会网络计算基础理论与实践.pdf]]P67+7
  - 代码可参见[[R语言社会网络分析#计算四种中心性并返回数据框]]
强弱关系
- [[高斯混合模型（GMM)]]
- 参考文献
- 弱关系和捷径的关系验证
  - 邻里重叠度（Jaccard相似度）：两节点共同邻居结点数/两节点邻居的总数

参考文献

Newman, M. E. J. (2003). The structure and function of complex networks (Vol. 45). Society for Industrial and Applied Mathematics. https://doi.org/10.1137/S003614450342480

van Eck, N. J., & Waltman, L. (2009). How to normalize cooccurrence data? An analysis of some well-known similarity measures. Journal of the American Society for Information Science and Technology, 60(8), 1635–1651. https://doi.org/10.1002/asi.21075